Probabilistic Topic Modeling with LDA

Python User Group Workshop

Markus Konrad markus.konrad@wzb.eu

January 2018

Material will be available at: http://dsspace.wzb.eu/pyug/topicmodeling1/

Outline

Today

  • Theory

    • What? Why? How?
    • Assumptions and prerequisites
    • LDA with the Gibbs Sampling algorithm

  • Practice – Using LDA for Topic Modeling

    • Software in the Python world and beyond
    • Common pitfalls

  • Literature

Next time

  • Example: A topic model for the parlamentary debates of the 18th German Bundestag
    • Data preparation
    • Model selection
    • Visualization and evaluation

What is Topic Modeling?

Topic modeling is a method to discover abstract topics within a collection of documents.

Each collection of documents (corpus) contains a "latent" or "hidden" structure of topics. Some topics are more prominent in the whole corpus, some less. In each document there are multiple topics covered, each to a different amount.

The latent variable $z$ describes the topic structure, as each word of each document is thought to be implicitly assigned to a topic.

What is LDA?

*Latent Dirichlet Allocation (LDA)* is a topic model that assumes:

  • each document is made up from a *mixture of topics*
  • each topic is a distribution over all words in the corpus

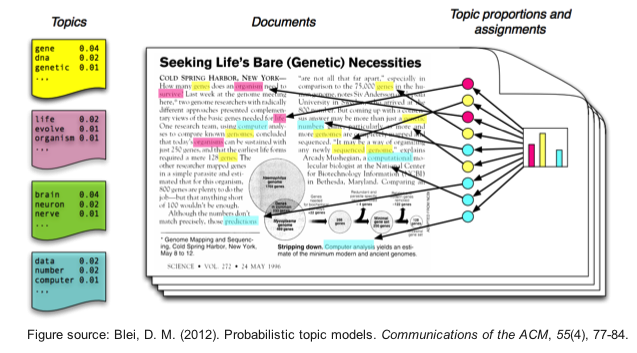
Example: Parlamentary debates

  • Which topics are exihibited? → mixture of words in topics
  • Who talks when about which topics? → mixture of topics in "documents" (i.e. debates)

Classic approach:

  • use meta-data when provided
    • TOPs in German Bundestag debates data not really usable – range from very specific ("Bundeswehreinsatz in Südsudan") to very general ("Fragestunde")
  • use human judgment
    • extremely time-consuming (~15,000 speeches; avg. ~400 words each)
    • sampling → easy to miss important documents/topics

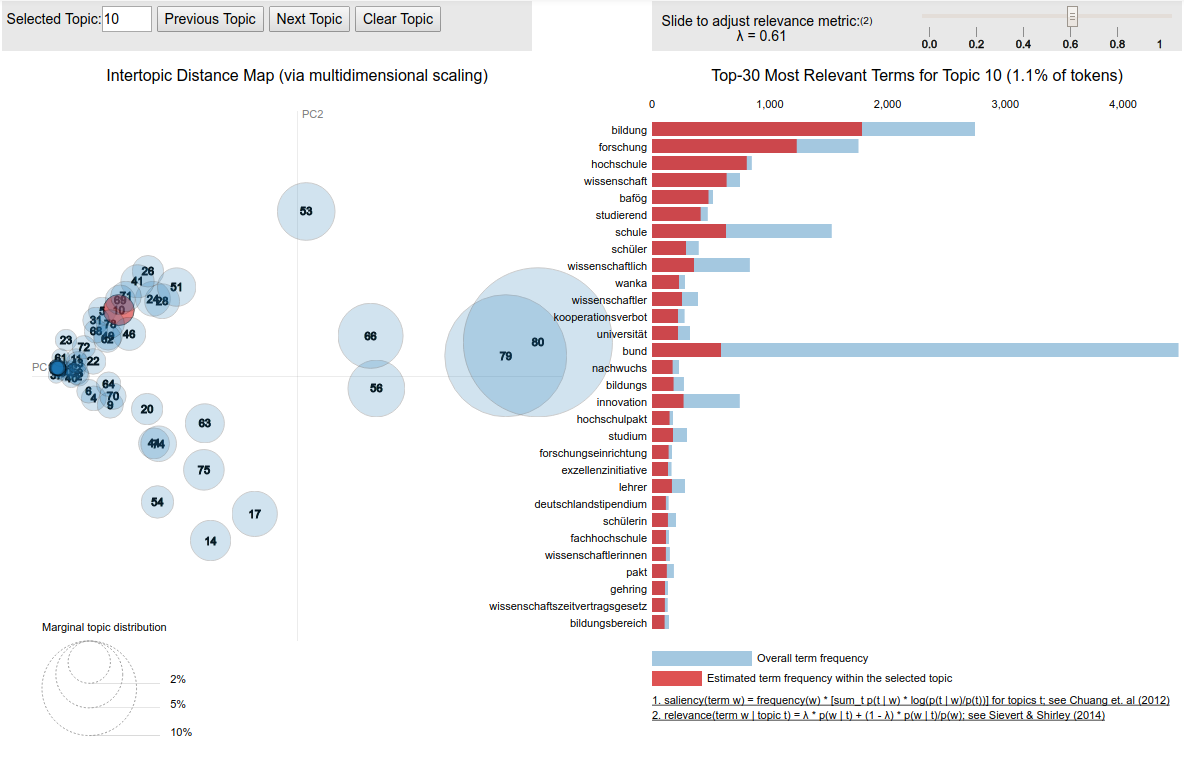
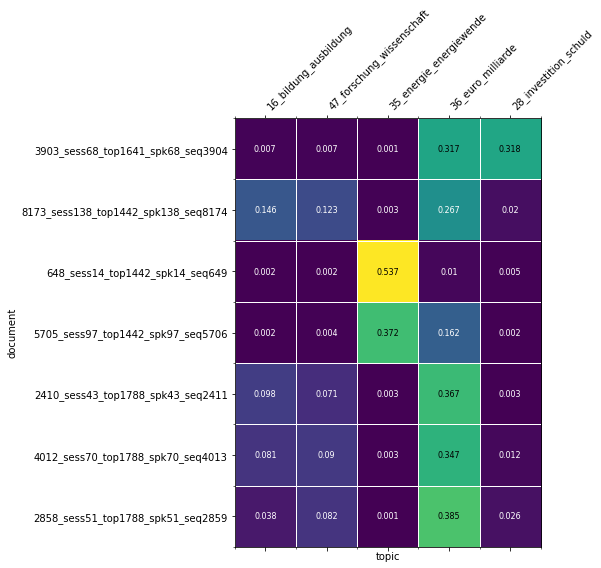
Why should I need that?

Corpus exploration

  • topic modeling originally invented for browsing large corpora
  • exploration / filtering by selecting topic(s) → show documents related to topic(s)
  • can be combined with visualization tools

Data analysis

  • topic proportions per document
  • topic shift over time
  • clustering of documents
  • networks of topics (topic co-occurrence, Wiedemann 2015)

Has been used successfully for hypothesis testing (Fligstein et al 2017)

Assumptions

  • **order of words in documents does not matter** → "bag of words" model
  • no relations between words → no context! → topics are "neutral" (**but:** context of words within topics can be interpreted)
  • documents can by anything: news articles, scientific papers, books, chapters of books, paragraphs
  • but: each document should convey a *mixture of topics* → problematic with very short documents (tweets)
  • **order of documents in a corpus does not matter**
  • **the number of topics $K$ is known (has to be set in advance)**
  • infer from the data by evalating the quality of a model (not today's topic)

Prerequisites

  • input text must be preprocessed:
    • tokenize: split sentence into separte "tokens" (~ words)
    • normalize: stemming, lemmatization (find word stems)
    • filter: remove stopwords, punctuation, etc.

Original: "In the first World Cup game, he **sat** only on the bank."

Tokens: first, world, cup, game, he, sit, bank

  • exact preprocessing steps (stopword removal, n-grams) domain specific!

Input: document-term-matrix (DTM)

  • tokens are converted to document term matrix (DTM) (according to "bag of words" model)
  • maps documents to word frequencies
document russia putin soccer bank
$D_1$ 3 1 0 1
$D_2$ 0 0 2 1
$D_3$ 0 0 0 2

The LDA topic model

An LDA topic model can be described by two distributions:

  • a document-topic distribution $\theta$: each document has a distribution over a fixed number of topics $K$
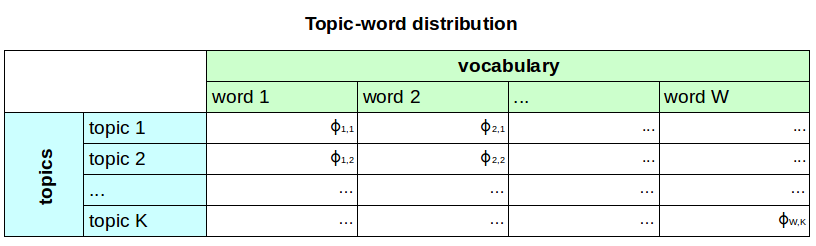
  • a topic-word distribution $\phi$: each topic has a distribution over a fixed vocabulary of $N$ words

Given this model, we can generate words:

  • for each document $d$ in a corpus $D$, generate each word $w$ like this:
    • draw a topic $t$ from a document-specific distribution over topics $\theta_d$
    • draw a word $w$ from a topic-specific distribution over words $\phi_t$

Finding the topic structure

two posterior distributions that can be calculated from latent variable $z$ (the assignments of a word in a document to a topic):

1. topic-word distribution $\phi$

→ describes the topics (which words are important for them)

Topic-word distribution $\phi$

Each topic has a distribution over all words in the corpus:

topic russia putin soccer bank possible interpretation
topic 1 0.5 0.4 0.0 0.1 russian politics
topic 2 0.1 0.0 0.7 0.2 soccer in russia
topic 3 0.3 0.0 0.0 0.7 russian economy
  • $K$ (num. of topics) distributions across $W$ words
  • topics are a mixture of words → have different weights on words
    • different meanings of words can be interpreted (soccer: "player sat on the bank" / economy: "banks in crisis")

2. document-topic distribution $\theta$

→ describes the documents (which topics are important for them)

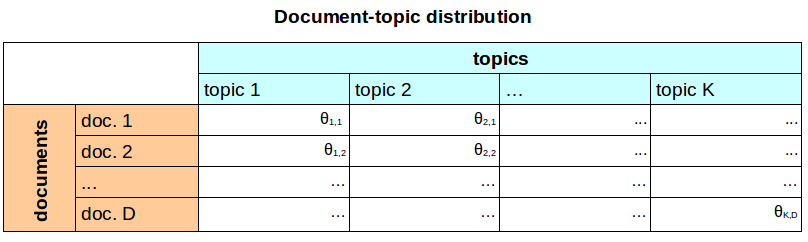
Document-topic distribution $\theta$

Each document has a different distribution over all topics:

document topic 1 topic 2 topic 3 possible interpretation
doc. 1 0.0 0.3 0.7 mostly about soccer and russian economy
doc. 2 0.9 0.0 0.1 russian politics and a bit of economy
doc. 3 0.3 0.5 0.2 all three topics
  • $D$ (num. of documents) distributions across $K$ topics
  • documents are a mixture of topics, each to a different proportion

Estimating $\phi$ and $\theta$

direct calculation not possible (involves $K^n$ terms with $n$ being num. tokens in corpus) (Griffiths & Steyvers 2004)

estimations either with:

  • Expectation-Maximization algorithm – an optimization algorithm (Blei, Ng, Jordan 2003)
  • Gibbs sampling algorithm – a "random walk" algorithm (Griffiths & Steyvers 2004)

both are rather complicated algorithms

LDA with Gibbs sampling

  • $K$ .. num. topics
  • $D$ .. documents
  • $Z$ .. assigns a word $w$ in a document $d$ to a topic $t \in [1, K]$

Algorithm uses iterative resampling

First: initialize a random $Z$ – each word is randomly assigned to a topic

LDA with Gibbs sampling

  • repeat for many iterations*:
  • for each document $d$ in $D$ and each word $w$ in $d$:
    • calculate sampling probability $p(z*)$ for drawing new topic for $w$
      • depends on current topic assignments of all other words ($Z_{\lnot\{d,w\}}$)
      • $p(z*) = p(w|z) p(z|d)$
        • $p(w|z)$: how likely is $w$ for each topic assignment $z$
        • $p(z|d)$: how likely is each topic assignment $z$ for $d$
    • sample a new topic assignment $z*$ from $p(z*)$, set $Z_{d,w} = z*$

Finally determine $\phi$ and $\theta$ from current $Z$.

* depends on corpus size (~1000 iterations is usually fine – log-likelihood must converge)

LDA with Gibbs sampling

supplementary tm_toy_lda notebook shows step-by-step implementation

Important take-aways:

  • Gibbs sampling is a random process
    • converges after some iterations (can be assessed with log-likelihood)
    • each time you run the algorithm, the results will slightly differ*
    • topic numbers will be completely different → they do not say anything!*
  • hyperparameters need to be set in advance:
    • number of topics $K$
    • concentration parameters $\alpha$ and $\beta$

* unless your random number generator is manually set to a certain state and your data and hyperparameters are the same

Concentration parameters $\alpha$ and $\beta$

  • $\alpha$ and $\beta$ specify prior beliefs about sparsity of topics ($\alpha$) and words ($\beta$)
  • both parameters are concentration parameters for *Dirichlet* distributions used as priors
  • $\alpha$ defines Dirichlet priors of $\theta$
  • $\beta$ defines Dirichlet priors of $\phi$
  • both are usually *symmetric*, i.e. a scalar value putting equal weight on words and topics respectively
  • *asymmetric* priors: weight on certain words/topics
  • [Wallach et al. (NIPS 2009)](http://papers.nips.cc/paper/3854-rethinking-lda-why-priors-matter) show that asymmetric priors on $\phi$ are not recommendable, but can be favorable on $\theta$
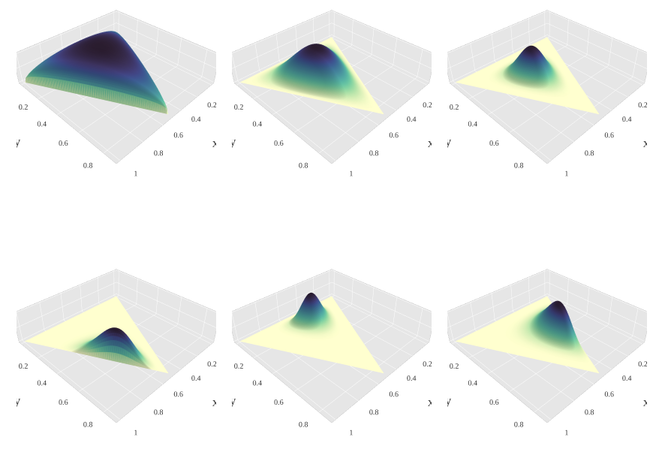Dirichlet distributions with concentration paramaters in clock-wise order: (1.3,1.3,1.3), (3,3,3), (7,7,7), (2,6,11), (14,9,5), (6,2,6) – [source](https://en.wikipedia.org/wiki/File:Dirichlet-3d-panel.png)

Concentration parameters $\alpha$ and $\beta$ in practice

$\alpha$ as prior belief on sparsity of topics in the documents:

  • when using **high $\alpha$**: each document covers many topics (lower impact of topic sparsity)
  • when using **low $\alpha$**: each document covers only few topics (higher impact of topic sparsity)
  • $\alpha$ is often set to a fraction of the number of topics $K$, e.g. $\alpha=1/K$ → with increasing $K$, we expect that each document covers fewer, but more specific topics

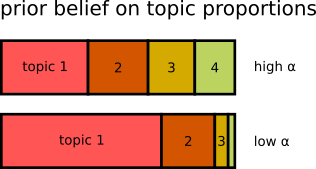
$\beta$ as prior belief on sparsity of words in the topics

  • when using **high $\beta$**: each topic consists of many words (lower impact of word sparsity) → more general topics
  • when using **low $\beta$**: each topic consists of few words (higher impact of word sparsity) → more specific topics
  • $\beta$ can be used to control "granularity" of a topic model
    • high $\beta$: fewer topics, more general
    • low $\beta$: more topics, more specific

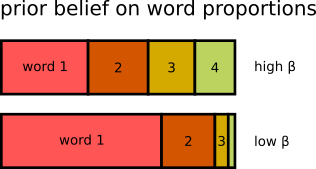
Impact of $\beta$

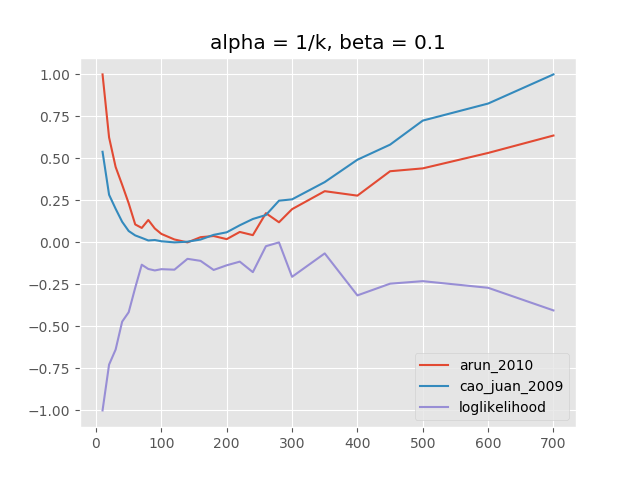high $\beta$ – good number of topics between 100 and 200
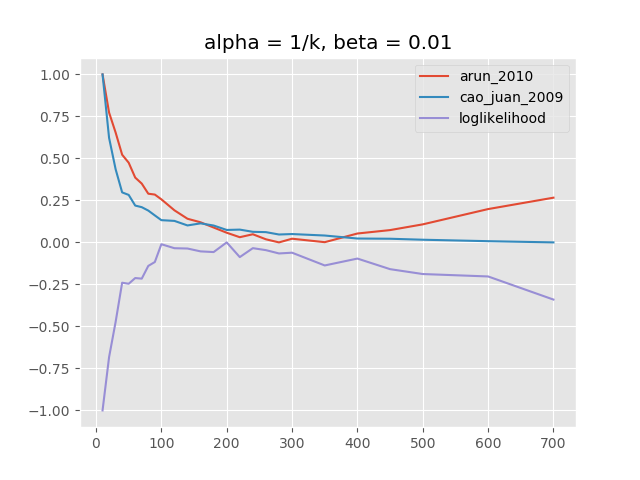low $\beta$ – good number of topics between 200 and 400

Note: x-axis is number of topics, y-axis is normalized scale for different "model quality" metrics

Practice – Using LDA for Topic Modeling

Software

  • Python packages:
    • lda – fast Gibbs sampling implementation
    • implementations using Expectation-Maximization / Variational Bayes:
  • other software:

Considerations before using LDA / common pitfalls

Problem: Your data does not meet the assumptions for LDA, e.g.:

  • documents are too short (e.g. tweets, chat messages): no mixture of topics
  • corpus consists of few but very long documents (e.g. a collection of Tolstoy novels): too few information shared across documents
  • corpus consists of documents of very different lengths (e.g. collection of tweets and Tolstoy novels): big documents dominate topics; both of the above problems
  • order of documents does matter (e.g. ordered by time)

Solutions:

  • merge documents where possible (e.g. combine all tweets of a user per week)
  • split documents where possible (e.g. split novels by chapters/paragraphs/etc.)
  • use alternative algorithm (Gibbs sampling vs. Variational Bayes approach)
  • use other approach than (classic) LDA

Problem: You do not know which priors to set (num. topics $K$, $\alpha$, $\beta$)

  • evaluate models with different hyperparameter sets using model quality metrics (covered in a later session)
  • use automatic hyperparameter optimization for $\alpha$, $\beta$ like in MALLET
  • use a non-parametric alternative to classic LDA

Problem: A lot of uninformative words appear in my topics

  • use stopword lists to remove very common words from the corpus

Problem: Some topics are very general and uninformative

  • LDA tends to create some very general topics with most common words
  • as long as it is only a few topics: ignore them in further analysis
  • otherwise improve stopword list and adjust hyperparameters

Problem: Computing the models takes very long

  • calculate several models in parallel on a multi-processor machine (e.g. WZB's theia machine)

Problem: Out of memory errors (corpus is too big for memory)

  • make sure to use sparse matrices as data structures
  • use software like Gensim that can stream data from hard disk

Alternatives to classic LDA for Topic Modeling

Latent Semantic Analysis (LSA) and Non-negative Matrix Factorization (NMF)

  • can be helpful when the assumptions for LDA are not met
  • input does not have to be integer data (e.g. tf-idf transformed data can be used)
  • do not require hyperparameters (i.e. no prior beliefs must (or can!) be specified)
  • output is usually not as easy to interpret as the posterior distributions obtained from LDA

Extensions to LDA

Literature

Introductionary

LDA